Der Unterschied zwischen „A priori“ und „Axiom“ erklärt

Die Begriffe „a priori“ und „Axiom“ sind beide in der Philosophie und Logik wichtig, aber sie stehen für unterschiedliche Konzepte:

A Priori

Der Begriff „a priori“ bezieht sich auf Wissen oder Rechtfertigungen, die unabhängig von der Erfahrung sind. „A priori“-Wissen basiert auf logischen Schlussfolgerungen und nicht auf empirischen Beweisen. Im Gegensatz dazu steht das „a posteriori“-Wissen, das sich aus Erfahrungen oder empirischen Beweisen ableitet. Die Aussage „Alle Junggesellen sind unverheiratet“ gilt zum Beispiel als a priori, weil ihre Wahrheit durch das Verständnis der Definitionen der beteiligten Wörter erkannt werden kann, ohne dass der Familienstand aller Junggesellen untersucht werden muss.

Ein weiteres Beispiel für „A priori“-Wissen ist die mathematische Wahrheit 7 + 5 = 12. Diese Aussage gilt als a priori, weil ihre Wahrheit allein durch logisches Denken erkannt werden kann, ohne dass sie empirisch überprüft werden muss. Im Gegensatz zu empirischen Fakten, die sensorische Erfahrungen oder Beobachtungen erfordern (z. B. die Aussage „Der Himmel ist blau“), kann die Wahrheit von „7 + 5 = 12“ durch das Verständnis der Konzepte von Zahlen und Addition bestimmt werden, unabhängig von physischen Erfahrungen oder Beobachtungen. Diese Eigenschaft macht sie zu einem eindeutigen Beispiel für Wissen, das unabhängig von empirischen Beweisen ist und das Wesen des apriorischen Denkens verkörpert.

Axiom

Ein Axiom ist ebenfalls eine Aussage oder ein Prinzip, das ohne Beweis als wahr akzeptiert wird. Aber Axiome dienen als Grundbausteine, aus denen andere Wahrheiten innerhalb eines bestimmten Systems der Logik, Mathematik oder Theorie abgeleitet werden können. Sie gelten als selbstverständlich und werden verwendet, um weitere Wahrheiten oder Theoreme abzuleiten. In der Mathematik ist zum Beispiel die Aussage „Durch zwei beliebige Punkte gibt es genau eine Gerade“ ein Axiom der euklidischen Geometrie.

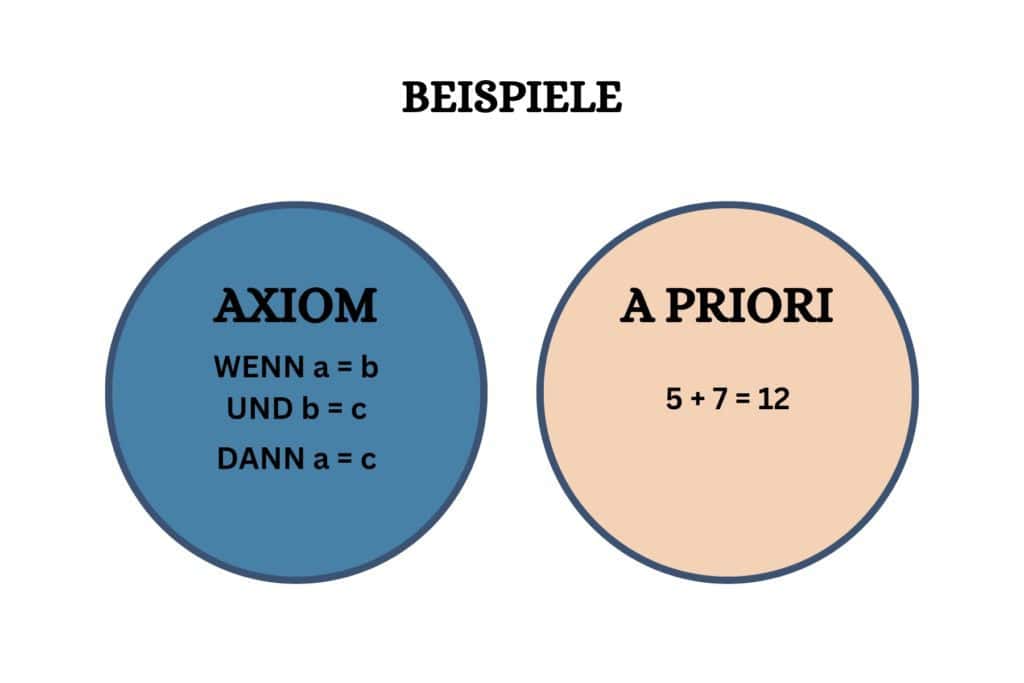
Ein anderes Beispiel für ein Axiom im Bereich der Mathematik ist das Gleichheitsaxiom, das besagt, dass wenn a = b und b = c, dann a = c. Dieses Axiom ist grundlegend für das Denken in der Mathematik, weil es ein grundlegendes Prinzip der Gleichheit festlegt, das ohne Beweis akzeptiert wird. Es bildet die Grundlage für viele mathematische Operationen und Beweise und dient als Ausgangspunkt, von dem aus andere Sätze logisch abgeleitet werden können. Das Gleichheitsaxiom ist selbstverständlich und muss nicht empirisch bewiesen werden. Es spielt eine entscheidende Rolle in der Struktur der mathematischen Logik und Algebra.

Schlüsselunterschiede

• Ursprung der Gültigkeit: Die Gültigkeit einer „A Priori“-Aussage ergibt sich aus der Logik oder der inhärenten Argumentation, ohne dass empirische Beweise erforderlich sind. Die Gültigkeit eines Axioms wird vorausgesetzt; es wird als Ausgangspunkt innerhalb eines bestimmten theoretischen Rahmens akzeptiert.
• Rolle in Wissen und Systemen: „A priori“-Wissen hilft bei der Unterscheidung zwischen Wissen, das durch Argumentation und Erfahrung gewonnen wird. Axiome dienen als Grundprinzipien, aus denen andere Aussagen innerhalb eines bestimmten Systems abgeleitet werden.
• Anwendungsbereich: A priori ist ein breiteres philosophisches Konzept, das auf Wissen im Allgemeinen anwendbar ist, einschließlich Mathematik, Logik und anderen Bereichen. Axiome werden vor allem in formalen Systemen wie der Mathematik, der Logik und den theoretischen Wissenschaften verwendet, da sie die ersten Wahrheiten darstellen, auf denen das System aufbaut.

Während es beim „A priori“-Wissen darum geht, wie wir etwas wissen (unabhängig von der Erfahrung), geht es bei einem Axiom um die grundlegenden Wahrheiten, auf denen ein logisches oder mathematisches System aufgebaut ist und die ohne Beweis akzeptiert werden.

Die beiden Konzepte sind auf Anhieb möglicherweise nicht leicht zu verstehen – zumindest ging es mir so – weshalb wir hier nochmal einen zweiten Anlauf, über einen anderen Winkel nehmen. Wir bedienen uns hier den jeweils zweiten Beispielen, die wir oben erwähnt hatten: das Gleichheitsaxiom und die mathematische Wahrheit. Wenn a = b und b = c, dann a = c auf der einen Seite und 5+7=12 auf der anderen.

Der wesentliche Unterschied zwischen einem Axiom wie dem Gleichheitsaxiom und apriorischem Wissen liegt in ihrer Rolle und in der Art und Weise, wie sie bei der Argumentation und beim Wissenserwerb eingesetzt werden:

Axiom: Ein Ausgangspunkt innerhalb eines Systems

• Kontextuelle Grundlage: Ein Axiom dient als Grundlage oder Ausgangspunkt innerhalb eines bestimmten Systems (z. B. Mathematik, Logik). Es wird innerhalb dieses Systems als wahr akzeptiert, ohne dass es bewiesen werden muss.
• System-spezifisch: Ihre Akzeptanz ist eher konventionell und hängt von den Regeln und Bedürfnissen des Systems ab, dem sie zugrunde liegen. Axiome werden verwendet, um die weiteren Sätze und Theoreme des Systems zu konstruieren und zu überprüfen.
• Zweck: Der Hauptzweck eines Axioms besteht darin, eine Grundlage zu schaffen, auf der ein kohärentes, in sich konsistentes System aufgebaut werden kann.

A-priori-Wissen: Unabhängigkeit von Erfahrung

• Universelle Anwendbarkeit: Im Gegensatz zu Axiomen, die systemspezifisch sind, beansprucht apriorisches Wissen eine universelle Gültigkeit, die nicht von den Regeln eines bestimmten theoretischen Systems abhängt.
• Begründungsgrundlage: A-priori-Wissen ist unabhängig von der Erfahrung gerechtfertigt. Sein Wahrheitsgehalt wird allein durch Überlegungen ermittelt, nicht durch empirische Überprüfung oder Beobachtung.
• Natur der Wahrheit: A-priori-Wahrheiten werden aufgrund ihrer logischen Form oder der inhärenten Natur ihrer Begriffe als notwendigerweise wahr in allen möglichen Welten angesehen.

Fazit

Der Hauptunterschied liegt in ihrer Anwendung und Begründung. Axiome sind grundlegende Wahrheiten, die innerhalb eines bestimmten Systems zum Zweck der Argumentation oder der Konstruktion dieses Systems angenommen werden. Sie sind wie die Regeln eines Spiels, auf die man sich geeinigt hat, um das Spiel der Mathematik oder Logik zu spielen. Das A-priori-Wissen hingegen bezieht sich auf Wahrheiten, die unabhängig von einem bestimmten System gültig sind. Sie werden durch Argumentation oder Logik abgeleitet, die sich nicht auf sensorische Erfahrungen oder empirische Daten stützt.

Das Axiom der Gleichheit ist ein spezifisches System der Mathematik und Logik, das eine notwendige Grundlage für Operationen und Beweise in diesen Disziplinen bildet. Im Gegensatz dazu wird apriorisches Wissen wie „7 + 5 = 12“ durch Schlussfolgerungen erkannt, die nicht von den Grundannahmen eines bestimmten Systems abhängen, sondern von der inhärenten Bedeutung von Zahlen und Addition.